Today I would like to talk about sound, as a good knowledge of it allows a better understanding of why a piano, though regularly and correctly tuned, does not always give satisfaction to its user.
How many times have I heard disappointed clients express this disillusioned thought: ”my piano is not as melodious as before”, and signify their reproach using a figurative expression: ”it sounds like a fiddle”, others, more precisely say “metallic” or “shrill” and some even consider parting with their piano.
Before resorting to this final solution, the tuner should be asked confirm if the instrument does not simply need to be reharmonised. Its tone has probably changed over time as a result of settling or worse, the wearing of the felt on the hammers which strike the strings. Often this work is neglected by some tuners claiming to be pianists but not having been trained, which demands long experience.
In terms of the tone to be obtained, the work of the harmoniser will be to make the felt more or less firm or more or less supple. If on the other hand these are too marked by the strings, they will need sanding down, or even replacing before beginning the work of pricking.
If the tone is too metallic, this involves increasing the aeration of the felt by pricking it in different places and depths according to the result obtained by using a special tool; felt which is less hard, will absorb the higher harmonics more easily and the tone obtained will be more rounded.
Conversely a tone which is too dull will be made brighter by impregnating the felt with a special product, left over from the process often used in the factory, to enable a demonstration piano to be listened to in a retail shop where the acoustics are such that the sound might appear more muffled. Lack of space has the inconvenience of absorbing more of the treble sounds than the bass, giving the instrument a duller, less flattering rendition, unlike large, empty rooms where the “railway station concourse effect” also known as the “cathedral effect” is very pronounced. Such a piano in all likelihood will be reharmonised, once delivered to the buyer’s house, above all if it is put in a large empty room (devoid of absorbent materials like carpets, curtains, large piece of furniture etc)
To understand in a more scientific way what this is all about:
- 1) What is sound ?
- 2) Characteristics of sound
- 3) Visualise a sound
- 4) Tone
- 5) Conclusion: harmonising
To help you to understand how the condition of the felt plays an essential role in the quality of the tone of your piano, I propose an experiment which is easy to carry out. With the back of a small spoon covered with self adhesive felt, strike a glass and it will make a dull sound. Repeat the operation having removed the felt and now the sound has become clearer, indeed clanging or metallic. You have just achieved, to some extent, what happens in the piano, but that is only a statement of fact and not an explanation. Also, I must now tell you about sound and its harmonics which give it its tone, and try to keep it simple with the use of diagrams and curves, avoiding complicated calculations. At least I will attempt to do this.
1) WHAT IS A SOUND ?
It is a hearing sensation produced by the regular vibrations of a body due to the impact of a shock, friction or all other mechanical causes, transmitted to the ear generally through the air. When these vibrations are irregular, they are unpleasant to hear and referred to as noise, for example: grinding, rumbling, popping, banging etc.
2) CHARACTERISTICS OF SOUND
A sound is defined by three parameters:
- The amplitude or its sound intensity measured in decibels (dB).
- The pitch also called frequency. It is the number of vibrations per second measured in hertz (Hz) or in periods per second (P.P.S.). A sound is called low between around 20 and 200 Hz. The more the frequency increases, the more high pitched it becomes. The audible limit for a normal ear does not exceed 18 to 20,000 Hz and diminishes with age.
- The tone is often called sonority. It is this which will make you understand the important role played by harmonisation. Tone gives a musical instrument its character. Thanks to this, it is possible to recognise by ear a particular instrument among others, playing the same note from the same octave. It is independent from the two parameters mentioned above and uniquely the consequence of these harmonics, which by their rank, phase and amplitude combined, give the sound its “colour” specifically called tone. Harmonics are the sound vibrations of a double, triple, quadruple frequency etc and always a complete multiple of the pure sound which gives the pitch (frequency). Knowledge of the shape of pure sound and harmonics allows us to understand how their combination changes the tone.
3) VISUALISE A SOUND
This can be done with laboratory equipment called cathode oscilloscopes when combined with a microphone. As this procedure is not available to everyone, a method can be used as described in secondary school physics books from the past.
- Take a piece of aluminium or glass.
- Blacken it with soot using a candle flame.
- Glue a bristle from a brush to the end of one of the of the points of a tuning fork.
- Vibrate the tuning fork, move it in a straight line with the bristle touching the soot and a curved line will be drawn.
The slower the movement, the tighter the curves will be and by appropriately choosing a high speed, a single curve can be achieved. Physicists and mathematicians called this sinusoid. In mathematics, we talk about the trigonometric function of the form f(x) = sine (x).
4) TONE (graphic explanation)
In order to explain how a pure sound acquires its tone by combining with one or several harmonics, we will take the simplest case: a single harmonic 2, that is to say double the frequency of its basic sound, which gives the pitch of the note . For example, for the LA3, 440 periods per second (PPS), the harmonic 2 will be LA4 880 PPS.
- Let’s trace figure 1, the curve representing pure sound.
- Let’s trace figure 2, the curve representing harmonic sound 2.
- Note for each one the two curves their respective sound intensities for different and the same increasing time values.
- Let’s trace figure 3, the curve representing the algebraic total of the sound intensity and of its two curves, that is to say taking account of the positive polarities of the higher alternations and the negative polarities of those which are lower (the result of the combination of fundamental sound distorted by harmonic sound 2.
| Time | Sound intensity curve1 | Sound intensity curve2 | Total of Sound intensity curve1 + curve2 |
Time | Sound intensity curve1 | Sound intensity curve2 | Total of Sound intensity curve1 + curve2 |
| 0 | 0 | 0 | 0 | 18,5 | – 0.90 | + 1,74 | + 0,84 |
| 0,5 | + 0,9 | + 1,74 | + 2,64 | 19 | – 1,74 | + 3,4 | + 1,66 |
| 1 | + 1,74 | + 3,40 | + 5,14 | 19,5 | – 2,60 | + 5,00 | + 2,40 |
| 1,5 | + 2,60 | + 5,00 | + 7,60 | 20 | – 3,40 | + 6,40 | + 3,00 |
| 2 | + 3,40 | + 6,40 | + 9,60 | 20,5 | – 4,23 | + 7,65 | + 3,42 |
| 2,5 | + 4,23 | + 7,65 | + 11,88 | 21 | – 5,00 | + 8,65 | + 3,65 |
| 3 | + 5,00 | + 8,65 | + 13,65 | 21,5 | – 5,73 | + 9,40 | + 3,68 |
| 3,5 | + 5,72 | + 9,40 | + 15,13 | 22 | – 6,40 | + 9,85 | + 3,45 |
| 4 | + 6,40 | + 9,85 | + 16,25 | 22,5 | – 7,10 | + 10,00 | + 2,90 |
| 4,5 | + 7,10 | + 10,00 | + 17,10 | 23 | – 7,65 | + 9,85 | + 2,20 |
| 5 | + 7,65 | + 9,85 | + 17,50 | 23,5 | – 8,20 | + 9,40 | + 1,20 |
| 5,5 | + 8,20 | + 9,40 | + 17,60 | 24 | – 8,65 | + 8,65 | 0,00 |
| 6 | + 8,65 | + 8,65 | + 17,30 | 4,5 | – 9,05 | + 7,65 | – 1,40 |
| 6,5 | + 9,05 | + 7,65 | + 16,70 | 25 | – 9,40 | + 6,40 | – 3,00 |
| 7 | + 9,40 | + 6,40 | + 15,80 | 25,5 | – 9,65 | + 5,00 | – 4,65 |
| 7,5 | + 9,65 | + 5,00 | + 14,65 | 26 | – 9,85 | + 3,40 | – 6,45 |
| 8 | + 9,85 | + 3,40 | + 13,25 | 26,5 | – 9,95 | + 1,74 | – 8,21 |
| 8,5 | + 9,95 | + 1,74 | + 11,69 | 27 | – 10,00 | 0,00 | -10,00 |
| 9 | + 10,00 | 0,00 | + 10,00 | 27,5 | – 9,95 | – 1,74 | -11,69 |
| 9,5 | + 9,95 | – 1,74 | + 8,21 | 28 | – 9,85 | – 3,40 | – 13,25 |
| 10 | + 9,85 | – 3,40 | + 6,45 | 28,5 | – 9,65 | – 5,00 | – 14,65 |
| 10,5 | + 9,65 | – 5,00 | + 4,65 | 29 | – 9,40 | – 6,40 | – 15,80 |
| 11 | + 9,40 | – 6,40 | + 3,00 | 29,5 | – 9,05 | – 7,65 | – 16,70 |
| 11,5 | + 9,05 | – 7,65 | + 1,40 | 30 | – 8,65 | – 8,65 | – 17,30 |
| 12 | + 8,65 | – 8,65 | 0,00 | 30,5 | – 8,20 | – 9,40 | – 17,60 |
| 12,5 | + 8,20 | – 9,40 | – 1,20 | 31 | – 7,65 | – 9,85 | – 17,50 |
| 13 | + 7,65 | – 9,85 | – 2,20 | 31,5 | – 7,10 | – 10,00 | – 17,10 |
| 13,5 | + 7,10 | – 10,00 | – 2,90 | 32 | – 6,40 | – 9,85 | – 16,25 |
| 14 | + 6,40 | – 9,85 | – 3,45 | 32,5 | – 5,72 | – 9,40 | – 15,13 |
| 14,5 | + 5,73 | – 9,40 | – 3,68 | 33 | – 5,00 | – 8, 65 | – 13,65 |
| 15 | + 5,00 | – 8,65 | – 3,65 | 33,5 | – 4,23 | – 7,65 | – 11,88 |
| 15,5 | + 4,23 | – 7,65 | – 3,42 | 34 | – 3,40 | – 6,40 | – 9,80 |
| 16 | + 3,40 | – 6,40 | – 3,00 | 34,5 | – 2,60 | – 5,00 | – 7,60 |
| 16,5 | + 2,60 | – 5,00 | – 2,40 | 35 | – 1,74 | – 3,40 | – 5,14 |
| 17 | + 1,74 | – 3,40 | – 1,66 | 35,5 | – 0,90 | – 1,74 | – 2,64 |
| 17,5 | + 0,90 | – 1,74 | – 0,84 | 36 | 0,00 | 0,00 | 0,00 |
| 18 | 0,00 | 0,00 | 0,00 |
Of the three curves being traced, it can be seen that the curve in figure 3 does not have the shape of a pure sinusoid like figures 1 and 2. It is distorted. This curve, being the combination of curves figures 1 and 2, which represent very true sounds, the sound corresponding to figure 3 of necessity can only be distorted. It is said that this sound is the result of specific colouring of pure sound by harmonic 2 or although it has acquired a tone.
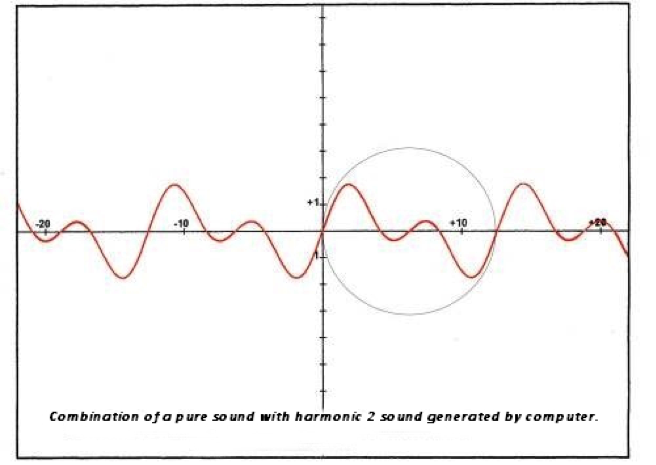
See below for the same curve as figure 3 traced by hand, but this time with the help of a computer. It is more regular than the manual curve, which on the other hand has had the advantage of being able to explain how sounds and harmonics are combined to make the tone without resorting to mathematics, which I undertook to do at the beginning. The similarity between the curves obtained graphically and by computer is noted with satisfaction.
5) CONCLUSION : HARMONISATION
Having said what is essential about sound, we will define the harmonisation of a piano. In the graphic demonstration, we saw how a pure sound was distorted when combined with harmonic 2, a choice dictated by the ease of the point by point manual tracing of the curves, figures 1,2 and 3.
Yet in fact, your piano generates not only harmonic 2 but also 3, 4, 5, etc., corresponding respectively to triple, quadruple frequencies etc., where sound densities and dephasing (time differences) between them, in relation to fundamental sound, give the instrument its specific tone. We have seen it in paragraph 2, these harmonics are multiple frequencies of fundamental sound, increasingly raised and therefore increasingly high pitched. These sounds, in the absence of harmonisation, have a tone which is unpleasant, too metallic and too clanging. A selection is necessary in all these harmonics and that involves tricky and meticulous work by the harmoniser on the felts and hammers. With the experiment of the glass and the felt glued to a spoon (paragraph 3), we have already given a rough explanation of the role played by felt as a filter for high pitched frequencies.